Your bag is empty
Don't miss out on great deals! Start shopping or Sign in to view products added.
Shop What's New Sign inDon't miss out on great deals! Start shopping or Sign in to view products added.
Shop What's New Sign inDon't miss out on great deals! Start shopping or Sign in to view products added.
Shop What's New Sign in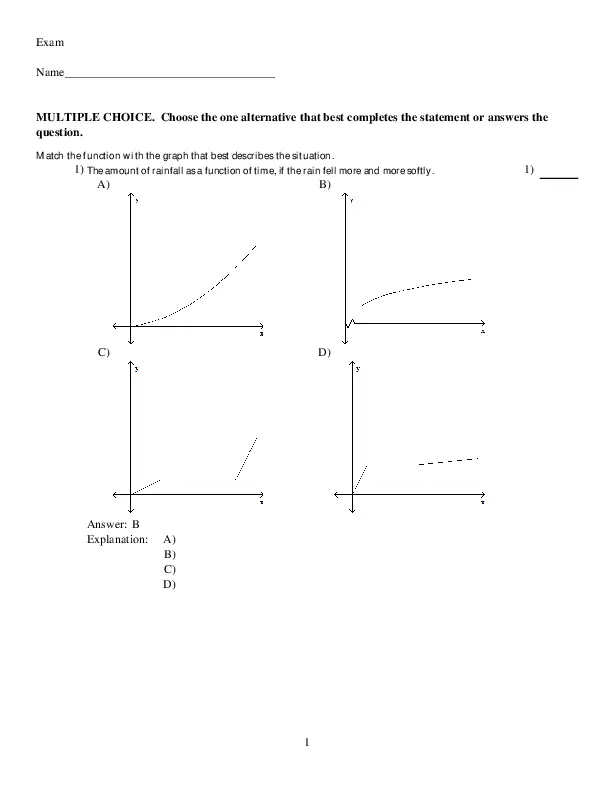
$18.99 $29.99Save:$11.00(37%)
0 (0 Reviews)






Don't miss out on great deals! Start shopping or Sign in to view products added.
Shop What's New Sign in
